网上实现AES的例子很多,但是错误的和遗漏的也很多,大概是一知半解的人和转载的人很多导致的,所以我打算自己撸一遍算法,以保证后续使用的时候既能保证正确又能开箱即用,也仅供其他人参考。
1. 算法流程
算法流程中,在之前的笔记中讲到的部分是:
- AES加密算法-密钥扩展;扩展密钥,加密过程给的原始密码不能用来直接去加密,要进行一系列步骤扩展成每一轮都是用的密钥,这个密钥不仅要求非线性(S盒替换),还要求密钥有一定的扩散(你可以是试着设置密码给1111,2222这样的密码来分析加密过程的对应关系)。
- AES加密算法-S盒构造;字节替换,非线形替换就是用S盒的值替换原来的值,这是加密部分唯一的非线形处理部分,这样明文和密文之间不会有一一对应的关系.
先贴具体的流程图,如下图参考: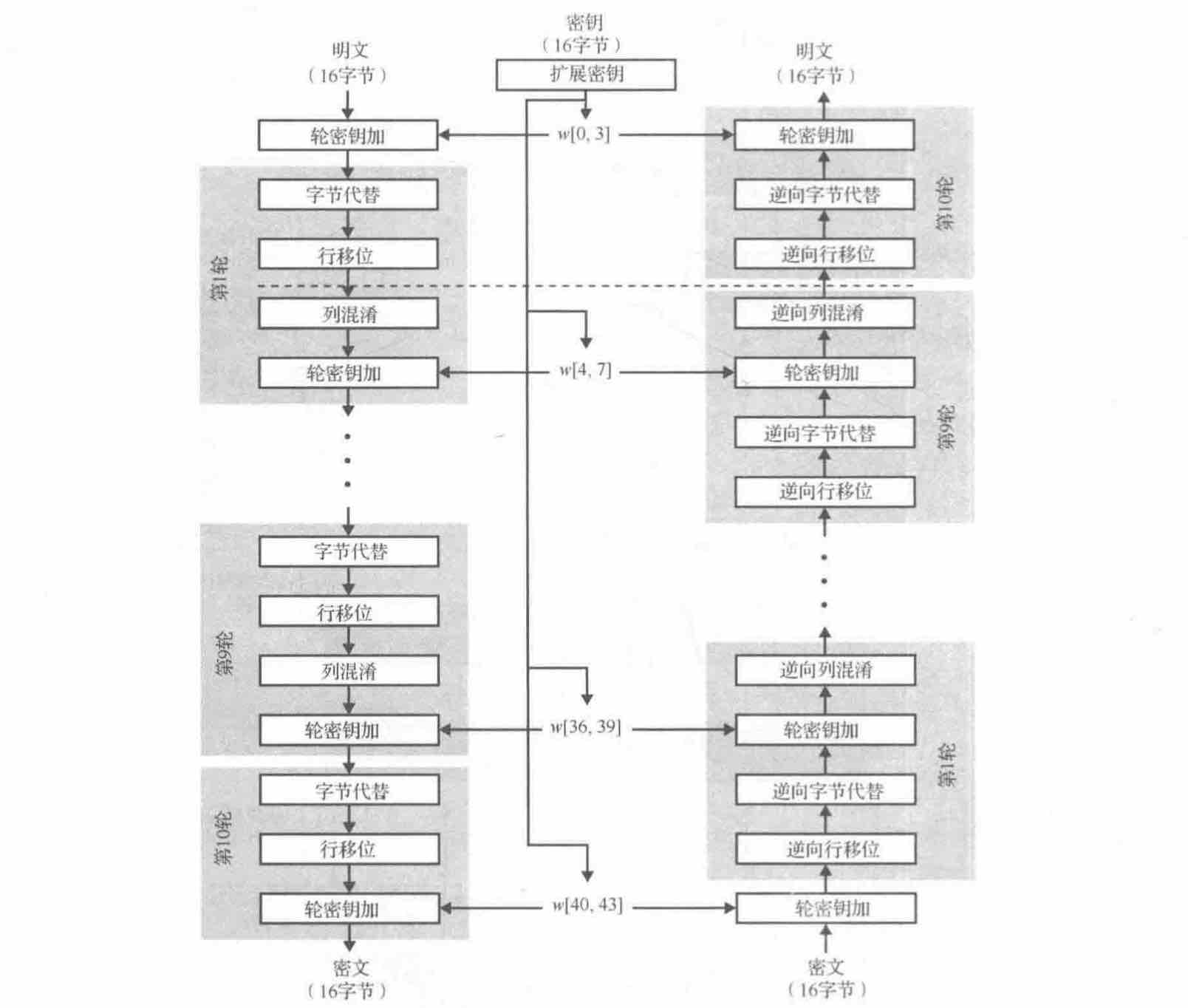
2. 单个步骤细节
行移位和列混淆以及轮密钥相加;皆是为了保证非线形处理后的密文不能存在一种数学上的线形特征。
2.1 循环行移位
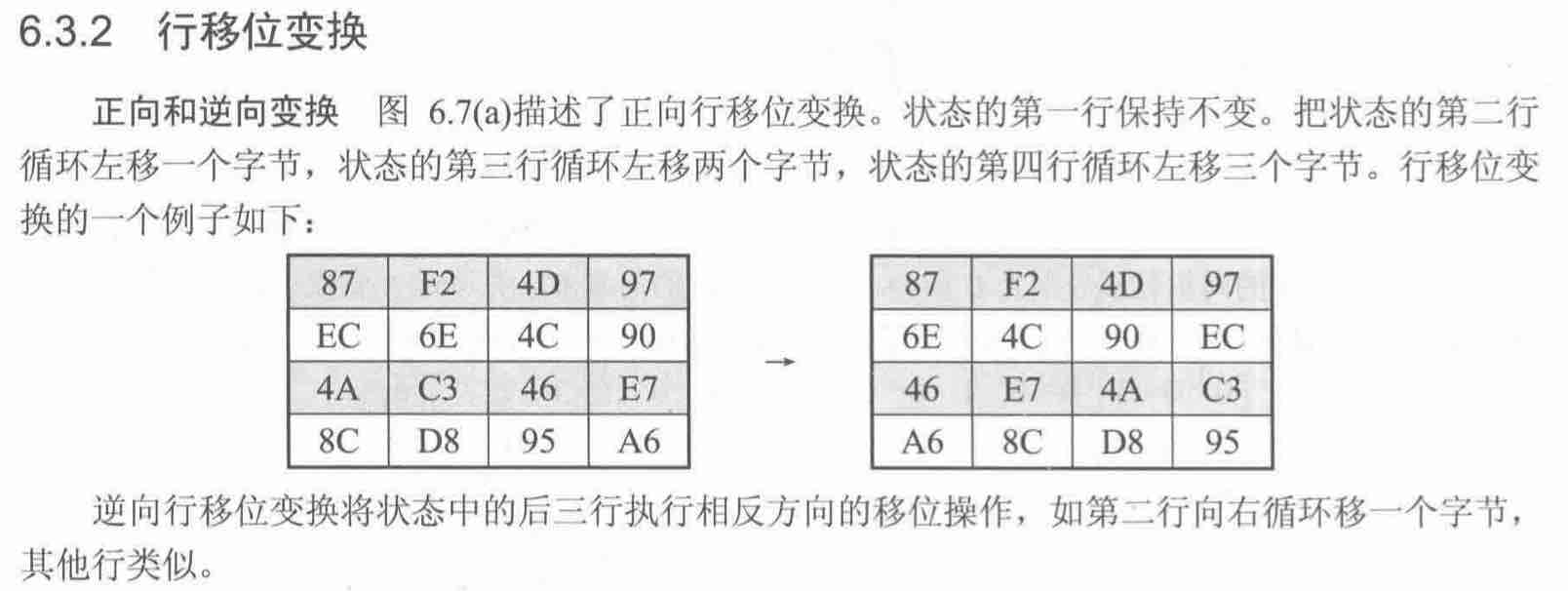
之前在密钥扩展的时候讲过循环左移位,不过那是四个字节的左移,这里是4x4的左移动,代码实现如下:
1 | void shift_rows(uint8_t *state) { |
2.2 列混淆
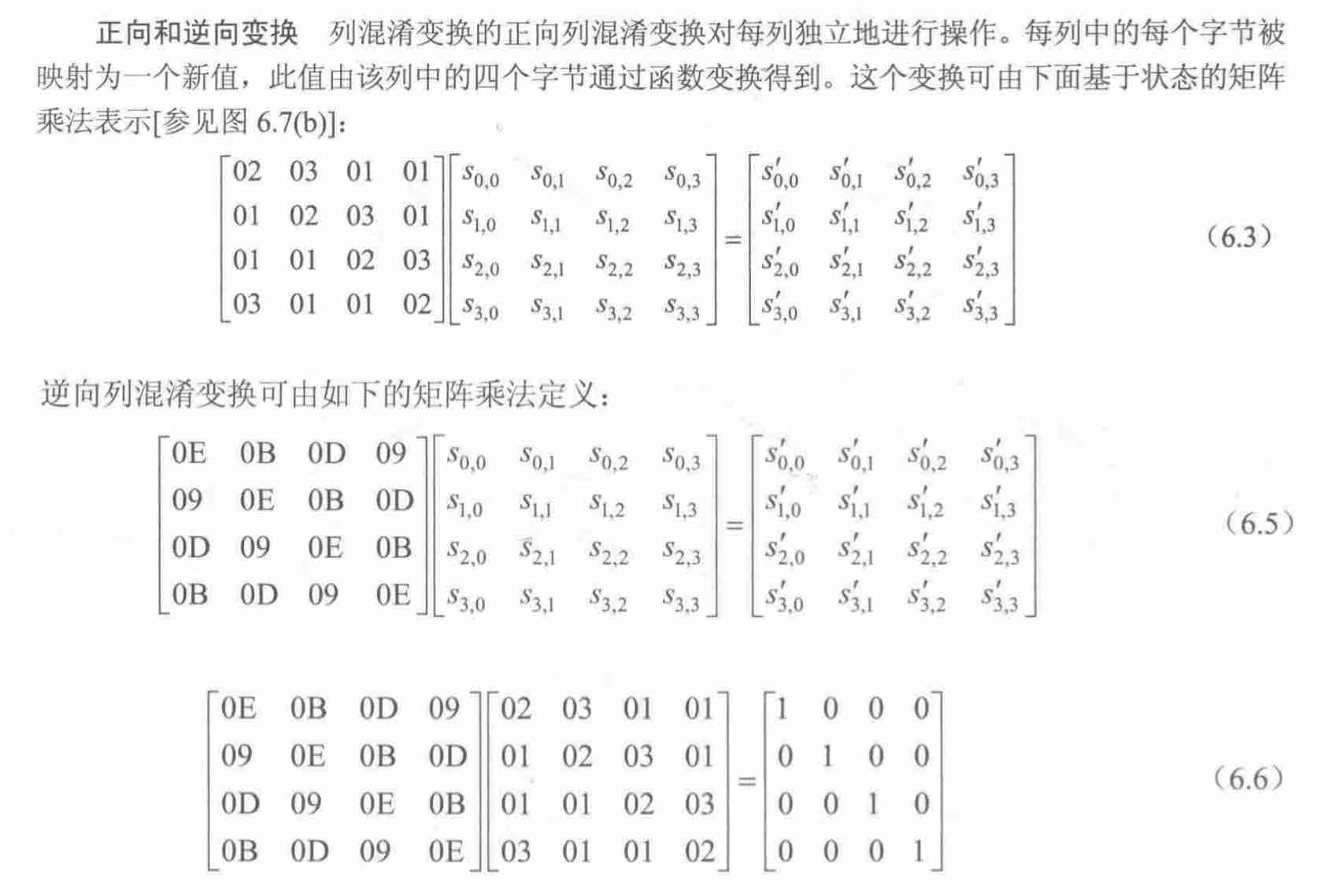
1 | // 列混淆 |
2.3 轮密钥相加
1 | // 这里是简单的4x4矩阵相加(XOR) |
2.4 字节替换(S盒替换)
之前密钥扩展时用到了字节替换(S盒替换),但那是一个4字节的替换,这里是4x4矩阵里逐个替换.
1
2
3
4
5
6
7
8
9
10
11
12
13
14 void sub_bytes(uint8_t *state) {
uint8_t i, j;
uint8_t row, col;
for (i = 0; i < 4; i++) {
for (j = 0; j < Nb; j++) {
// state对应位置的值作为行索引和列索引
row = (state[Nb*i+j] & 0xf0) >> 4;
col = state[Nb*i+j] & 0x0f;
state[Nb*i+j] = s_box[16*row+col];
}
}
}
3. 算法整体实现
3.1 加密流程
参考第一节流程图的代码实现如下:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40void cipher(uint8_t *in, uint8_t *out, uint8_t *w) {
// w的值为扩展密钥
uint8_t state[4*Nb];
uint8_t r, i, j;
// 直接将明文的4xNb字节初始化到state中.
for (i = 0; i < 4; i++) {
for (j = 0; j < Nb; j++) {
state[Nb*i+j] = in[i+4*j];
}
}
// 轮密钥相加
add_round_key(state, w, 0);
// Nr是轮数,128位加密是10轮,256位加密是14轮
// 这个轮数是可以增加的,论文中建议这么多轮
for (r = 1; r < Nr; r++) {
// S盒替换
sub_bytes(state);
// 循环左移动
shift_rows(state);
// 列混淆
mix_columns(state);
// 轮密钥相加
// 注意: 使用的w,根据r值不同而位置不同
// 密钥不同
add_round_key(state, w, r);
}
// 最后一轮的处理没有列混淆
sub_bytes(state);
shift_rows(state);
add_round_key(state, w, Nr);
// 将中间结果给out
for (i = 0; i < 4; i++) {
for (j = 0; j < Nb; j++) {
out[i+4*j] = state[Nb*i+j];
}
}
}
3.2 实例:
1 | int main() { |
附录:
4x4矩阵乘法,两个4x4的矩阵乘法,就是值等于各项乘积之和.1
2
3
4
5
6
7void coef_mult(uint8_t *a, uint8_t *b, uint8_t *d) {
// gmult是4字节与4字节的乘法
d[0]=gmult(a[0],b[0])^gmult(a[3],b[1])^gmult(a[2],b[2])^gmult(a[1],b[3]);
d[1]=gmult(a[1],b[0])^gmult(a[0],b[1])^gmult(a[3],b[2])^gmult(a[2],b[3]);
d[2]=gmult(a[2],b[0])^gmult(a[1],b[1])^gmult(a[0],b[2])^gmult(a[3],b[3]);
d[3]=gmult(a[3],b[0])^gmult(a[2],b[1])^gmult(a[1],b[2])^gmult(a[0],b[3]);
}