AES的密钥扩展是为了保证每轮加密使用的密钥的不同,要满足防止各种密码攻击的分析,有一定的步骤,这里和AES的加密一样,也用到了S盒,以保持非线性替代.
1. g函数计算步骤

2. 轮常量
参见AES加密算法-轮常量计算.md说明轮常量的计算过程,这个轮常量也是可以直接在代码中定义的。
3. 密钥扩展算法
- 第一步四个字节循环左移一位,定义位置变换函数rot_word(),作用是接受一个字 [a0, a1, a2, a3]作为输入,循环左移一个字节后输出[a1, a2, a3, a0]
1
2
3
4
5
6
7
8
9
10
11
12void rot_word(uint8_t *w) {
uint8_t tmp;
uint8_t i;
tmp = w[0];
for (i = 0; i < 3; i++) {
w[i] = w[i+1];
}
w[3] = tmp;
} - 第二步利用S盒进行字节替换
1
2
3
4
5
6
7void sub_word(uint8_t *w) {
// w的前两个字节为行索引,后字节值为列索引S盒替换
uint8_t i;
for (i = 0; i < 4; i++) {
w[i] = s_box[16*((w[i] & 0xf0) >> 4) + (w[i] & 0x0f)];
}
} - 第三步与轮常量相加(XOR),也就是两个四字节异或
1
2
3
4
5
6
7// d = a ^ b 按照字节进行异或
void coef_add(uint8_t a[], uint8_t b[], uint8_t d[]) {
d[0] = a[0]^b[0];
d[1] = a[1]^b[1];
d[2] = a[2]^b[2];
d[3] = a[3]^b[3];
}
4. 总体算法步骤
第一步是直接复制密钥的前四个字,每个字四个字节,第二部w[i]的值由w[i-1]和w[i-4]的异或得到(如下图w[5] = w[1]^w[4],w[6]=w[2]^w[5]),另外每排第一个又使用g函数处理(见1.g函数计算步骤)。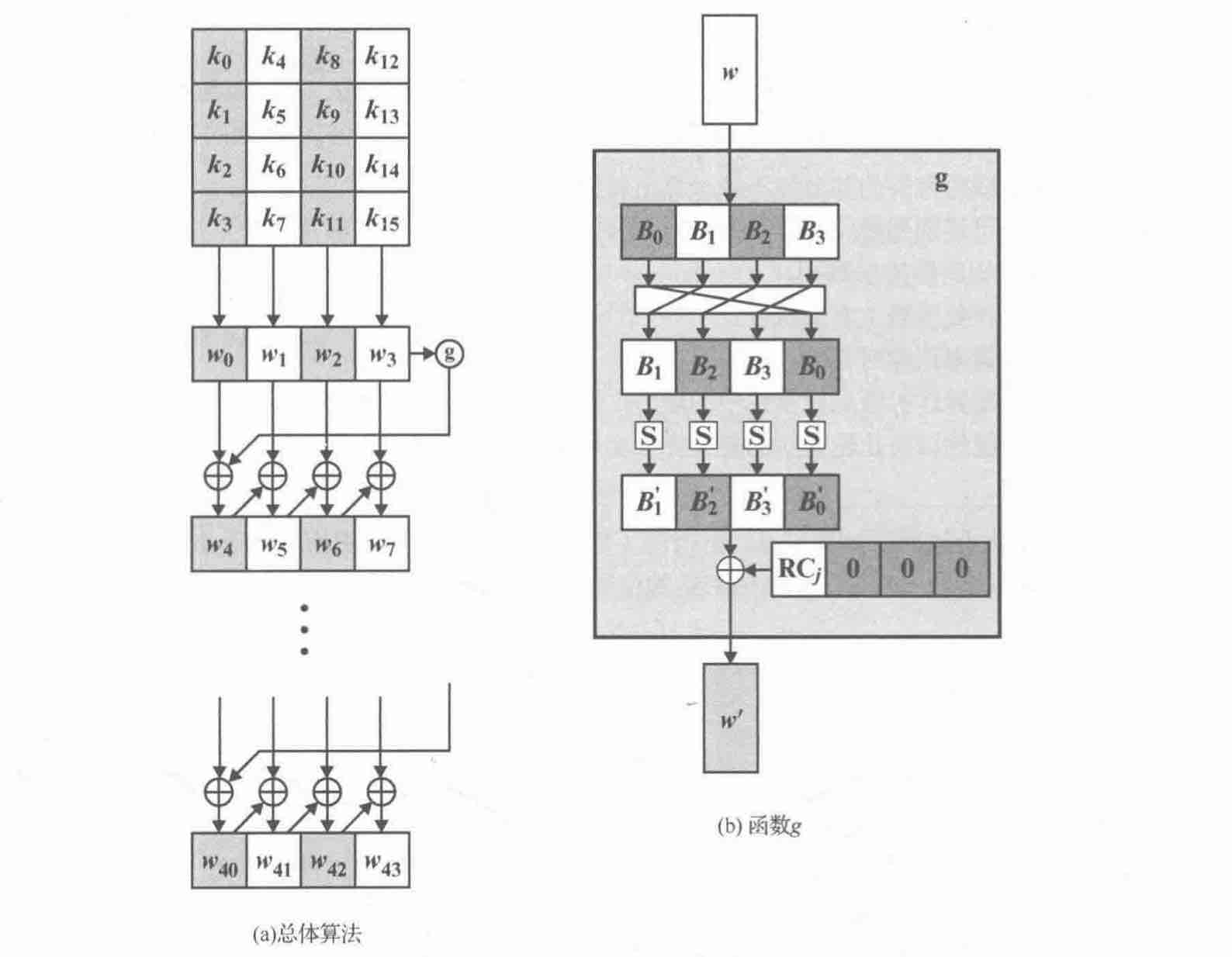
代码实现:1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45void key_expansion(uint8_t *key, uint8_t *w) {
uint8_t tmp[4];
uint8_t i, j;
uint8_t len = Nb*(Nr+1);
// 直接复制key的前4个字(16个字节)
for (i = 0; i < Nk; i++) {
w[4*i+0] = key[4*i+0];
w[4*i+1] = key[4*i+1];
w[4*i+2] = key[4*i+2];
w[4*i+3] = key[4*i+3];
}
// 扩展的密钥
for (i = Nk; i < len; i++) {
// 初始化tmp字
// tmp = w[i-1]
tmp[0] = w[4*(i-1)+0];
tmp[1] = w[4*(i-1)+1];
tmp[2] = w[4*(i-1)+2];
tmp[3] = w[4*(i-1)+3];
// 这里模Nk==0是g函数处理,==4时s盒替换
if (i%Nk == 0) {
// g函数处理
// 循环左移
rot_word(tmp);
// S盒替换
sub_word(tmp);
// 与轮常量异或
coef_add(tmp, Rcon(i/Nk), tmp);
} else if (Nk > 6 && i%Nk == 4) {
// 每四个字节 4 * uint8_t
// 直接S盒替换一个字
sub_word(tmp);
}
// 计算当前字的值
// w[i] = w[i-4] ^ w[i-1]
w[4*i+0] = w[4*(i-Nk)+0]^tmp[0];
w[4*i+1] = w[4*(i-Nk)+1]^tmp[1];
w[4*i+2] = w[4*(i-Nk)+2]^tmp[2];
w[4*i+3] = w[4*(i-Nk)+3]^tmp[3];
}
}