咖啡's blog

专心 专注 专业

0%

红黑树算法推导过程

发表于 更新于 分类于 ， Valine：

1. 2-3-4树的定义

定义:

  • 每个节点每个节点有 1、2 或 3 个 key ，分别称为 2- 节点，3- 节点，4- 节点。
  • 所有叶子节点到根节点的长度一致（也就是说叶子节点都在同一层）。
  • 每个节点的 key 从左到右保持了从小到大的顺序，两个 key 之间的子树中所有的 key 一定大于它的父节点的左 key ，小于父节点的右 key

首先2-3-4树为什么要叫做2-3-4树?
说明节点有3种:

  • 第一种是有两个孩子的：
  • 第二种是有3个孩子的：这里的空节点就先省略了，可见这种节点10和20在一个节点中，但也是按照一定的顺序排列的，并且5连接在10的左边，15连接在10和20中间，25在20右边
  • 第三种是有4个孩子的，这种就和第二种很像了，只不过节点中存放了3个值

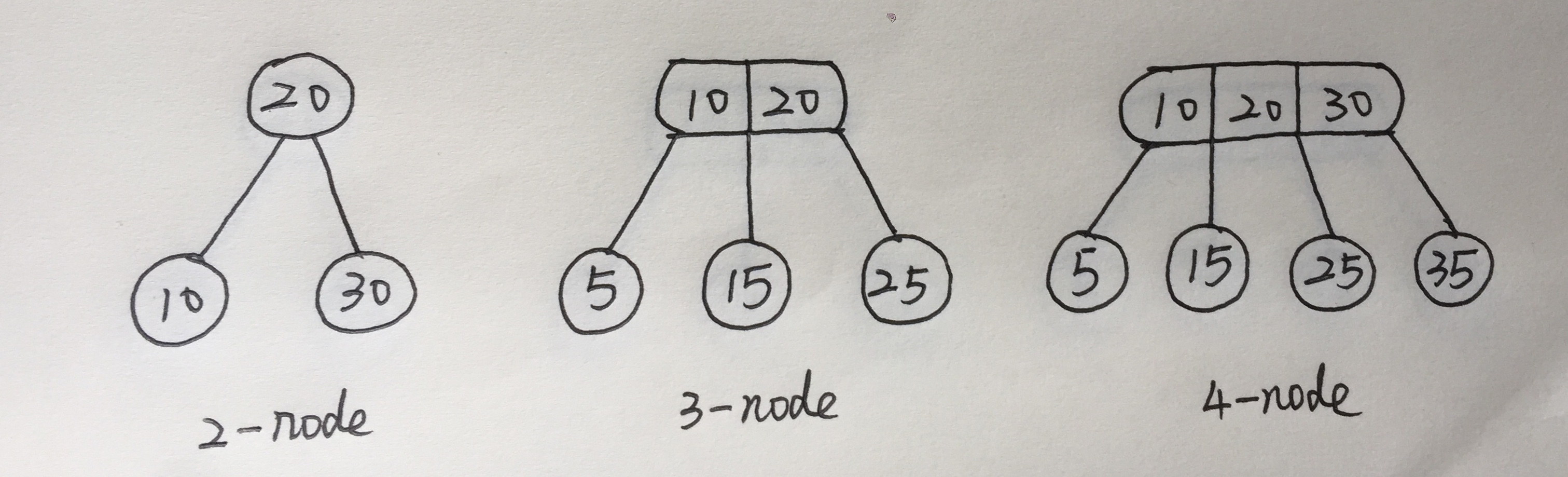
图中每个值连接的位置依然是有序的,2-3-4树中的非叶子节点就是由这三类节点构成的,同时2-3-4树还有一个特性是所有的叶子节点的深度都是相同的。这个是什么意思呢？就是所有的空节点的祖先的个数都是相同的，也意味着所有的非叶子结点的孩子必须连满。
举个例子:

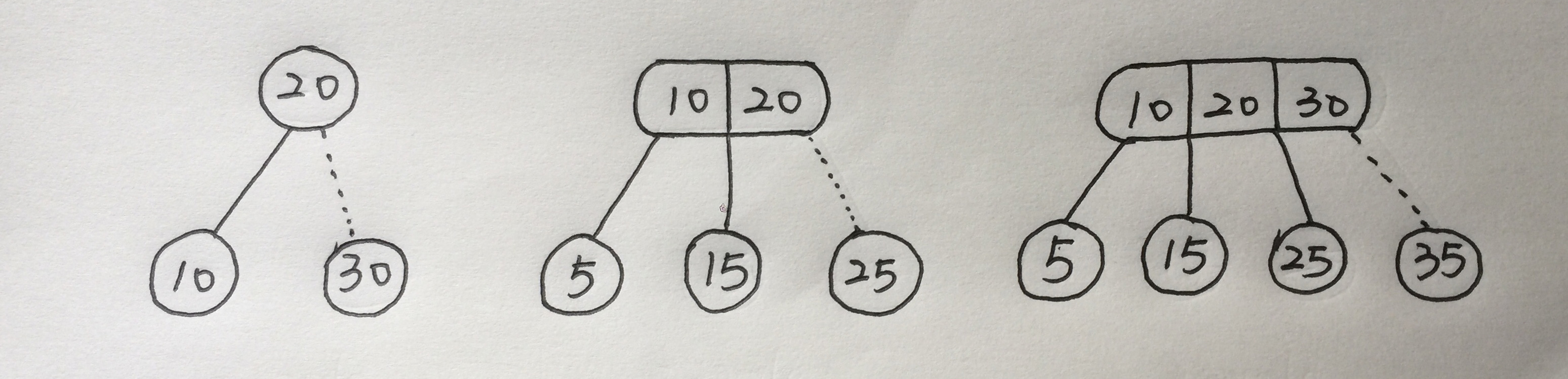
上面的三个图的虚线表示将被删除的结点，这些结点被删除以后，父节点没有连满，所以它就不是2-3-4树。这种情况会在节点删除的时候发生，之后就要做一些调整把它重新调整为2-3-4树。

2. 2-3-4树的删除操作举例

删除结点伴随着对不满足2-3-4树的情况进行调整
如下：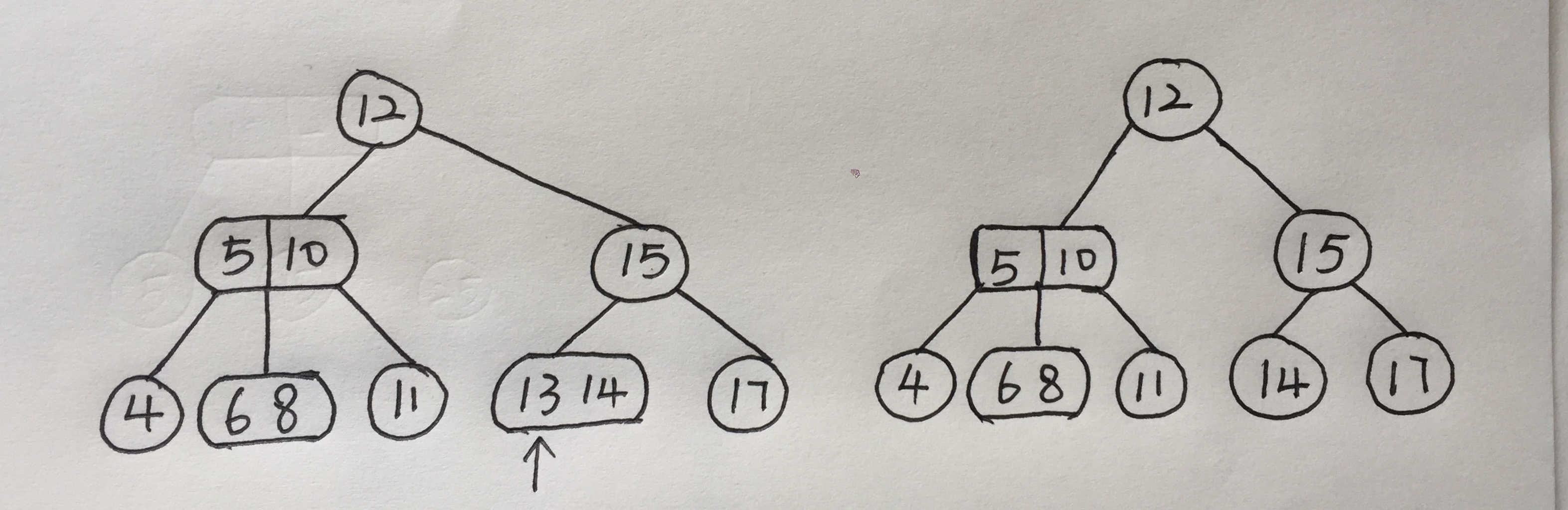

第一次删除13，当13没了的时候依然还是满足2-3-4树，所以不用调整

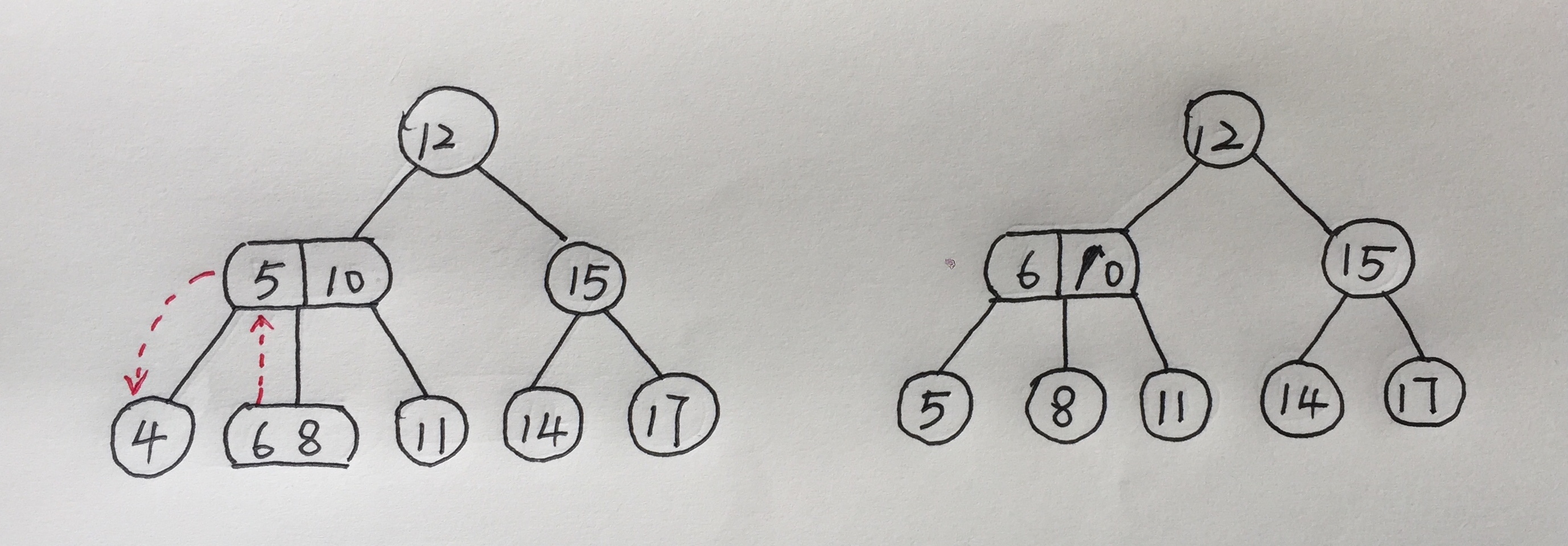
第二次删除4，当4没了的时候不满足2-3-4树的性质，于是找其兄弟节点是否有可以弥补的，所以找到了6上移，将5移下来，保持了叶子节点深度不变

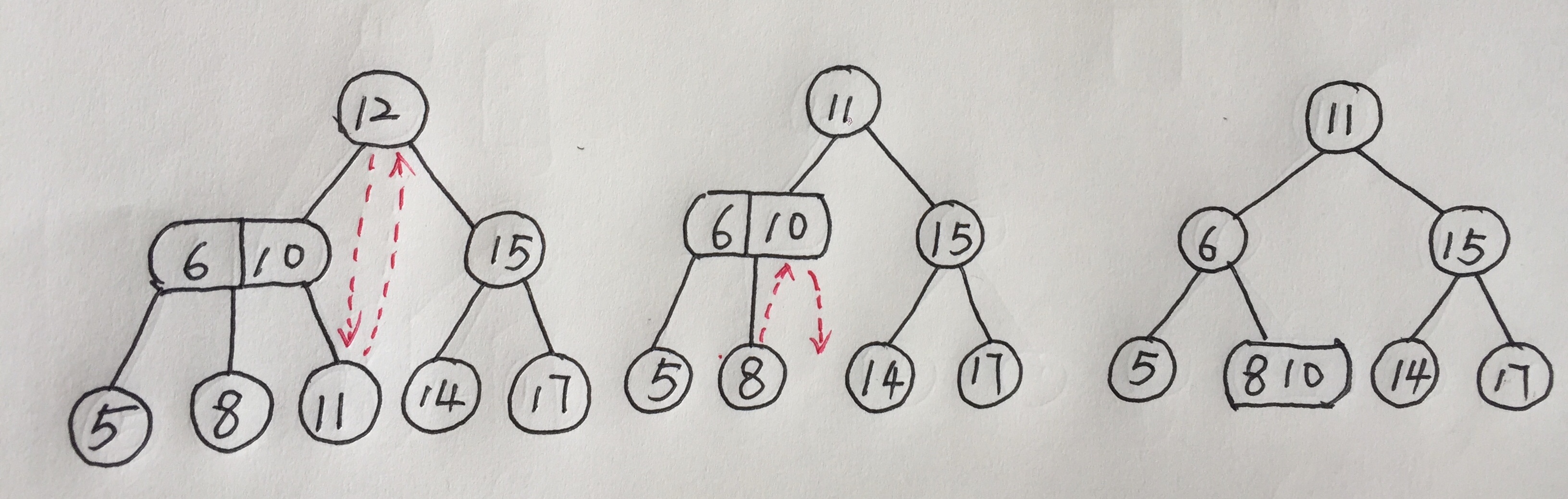
这次删除12,12是根节点，所以选择左子树最右边 代替他，11移走以后，就需要从父节点中把10移下来保持叶子结点的深度，同时把8和10合并。

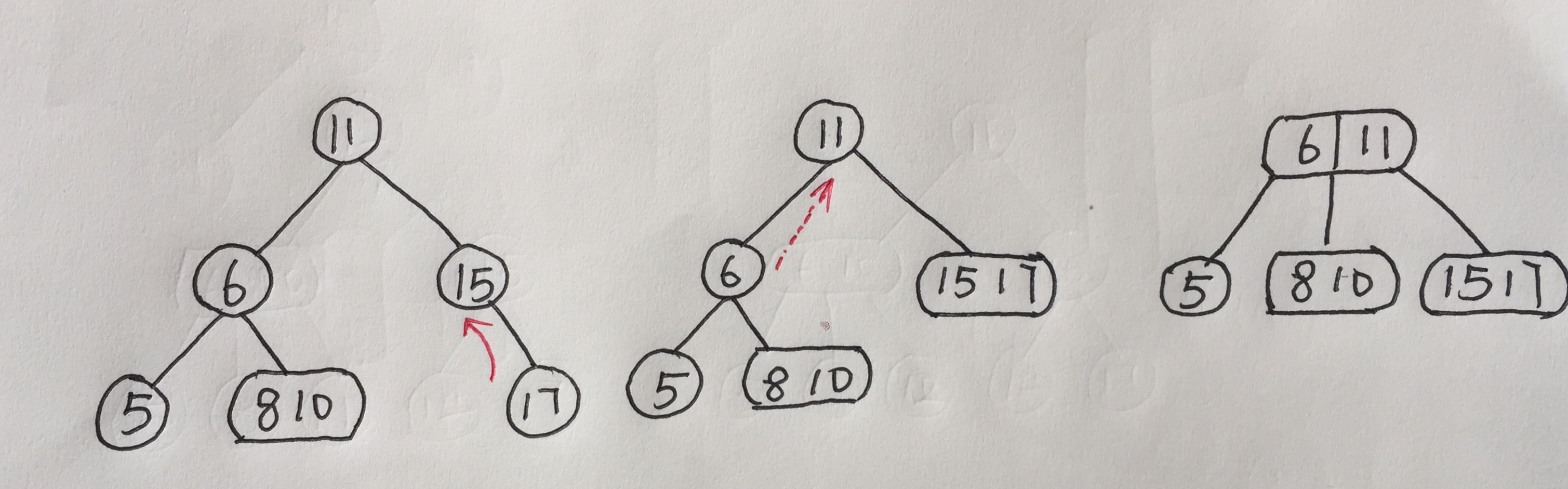
删除了14以后，要向父节点借结点,父节点再向兄弟结点借结点，以保持深度，但这个时候父节点和兄弟结点都为2-结点，所以合并；这时树的深度减一，所以要沿树向上调整高度，直到根结点结束，合并15，17结点后，当前结点的兄弟结点和父节点仍然为2-结点，这时6,11结点合并，调整完毕。

3. 2-3-4树删除的算法推导

3.1 删除非叶子结点

当删除的节点是非叶子节点，无论待删除节点的 key 是多少个，先使用中序遍历找到待删除节点的后继节点，然后将后继节点与待删除节点位置互换，此时就将问题转化为删除节点为叶子节点

3.2 删除叶子结点
  • 当前叶子结点多于1个key时，可以直接删除这个目标key
  • 当前叶子结点只有一个key时的处理转变成上一种情况，是需要向兄弟结点或者父亲结点借一个结点，以保证当前要删除的叶子结点多于1个key的情况，分为4种情况
    (1） 父节点为2结点，兄弟结点不为2结点，可借
    (2） 父节点为2结点，兄弟结点为2结点，父节点和兄弟结点合并(!!!需要调整树的高度)
    (3） 父节点不为2结点，兄弟结点不为2结点，可借
    (4） 父节点不为2结点，兄弟结点为2结点，可借(兄弟结点和一个父节点和当前结点合并为一个结点)
3.3 借结点

上面4种情况,只要父节点和兄弟结点不同时为2-结点的情况都可以借结点: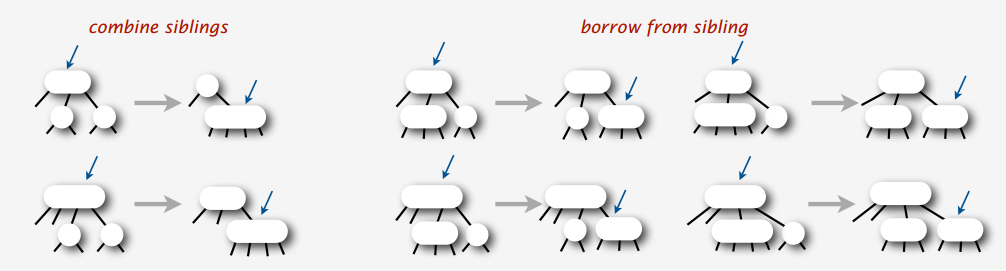

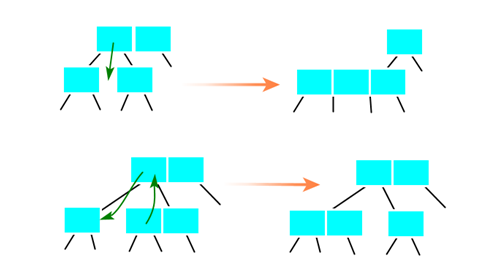
上面借结点的情况可以简化为两种情况:

  • 当前待删除结点从父节点借结点，父节点再从兄弟结点借一个结点
  • 当前待删除结点从父节点，父节点从兄弟那里借不到结点(兄弟结点为2-结点)
3.4 调整树高度

父节点和兄弟结点同时为2-结点时，父节点和兄弟结点合并，需要调整树高度的，调整树高度分为增加高度和减少高度的情况

  • 增加高度，只要能向父节点借到结点时，便将借到的结点变成当前待删除结点的父节点，增加高度(因为合并的时候减少了高度)
  • 减少高度,从父节点那里借不到结点时，说明父节点只能和兄弟结点合并，便减少了当前子树的高度，需要根据增加高度或者当前减少高度的规则，递归调整高度，直到根结点。
3.5 算法推导

我们如果要删除一个节点，把要删除的那个节点和这个结点的左子树的最大结点，或者这个结点的右子树的最小结点进行交换，那么删除任意结点就转换成删除叶子结点的情况。而删除叶子结点的情况，就是要保证叶子结点不是单独的key的结点(2结点),因为删除这个结点，将导致删除的结点的父节点不是一个2结点，或者说树的高度发生了变化。这个时候当带删除结点的key不为2结点时，直接删掉目标key；当带删除结点为2结点时，就需要向父节点借一个结点，父节点再向兄弟结点借一个结点，保证带删除结点为3结点或者4结点。借不到只有一种情况就是父节点和兄弟结点同时为2结点，这个时候合并向上调整整棵树的高度。

4. 红黑树的定义

透彻理解2-3-4树的定义以及删除过程是了解对应红黑树删除算法的前提。
定义:

  • 每个结点或红或黑
  • 根结点是黑色
  • 每个叶子结点是黑的
  • 如果一个结点是红色则两个儿子都是黑色
  • 对每个结点，从该结点到子孙结点的所有路径包含相同数目的黑色结点
4.1 红黑树与2-3-4树的等价关系

结点对应关系如下图:

根据结点对应图就可以将2-3-4树对应的红黑树为下图: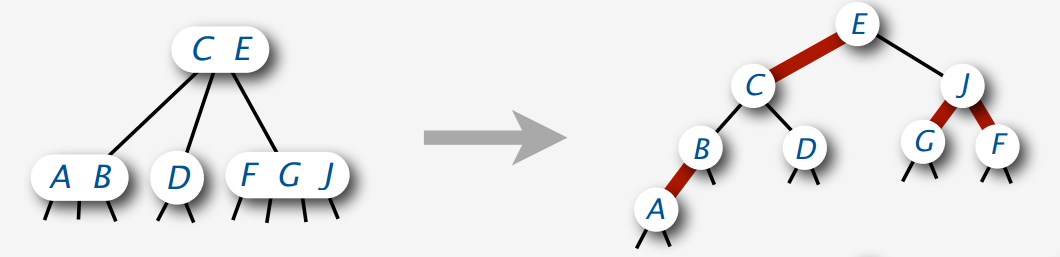

但是存在一个问题，就是对于一棵2-3-4树可能有多种不同的表示，这是在于对于3-node的表示，红色的边可以向左倾，也可以向右倾。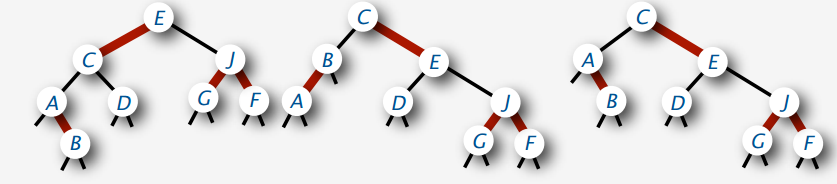

所以对于任何一棵2-3-4树，我们都可以得到一棵唯一对应的左倾红黑树，去掉3-结点的右倾对应的结点对应关系：

如果出现右倾的结点我们可以采取左旋的方法变成左倾，如图: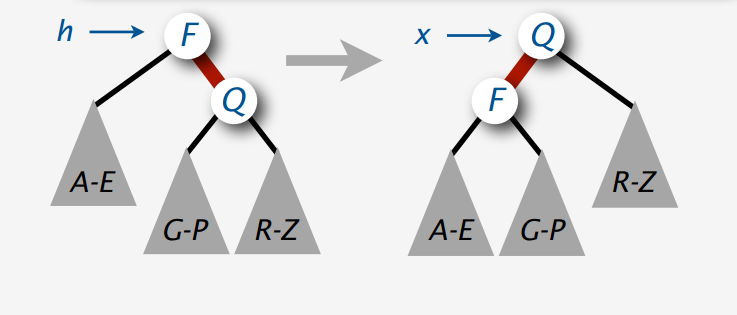

4.2 红黑树借结点与2-3-4树的借结点的等价

A结点的兄弟结点为2-结点的等价情况: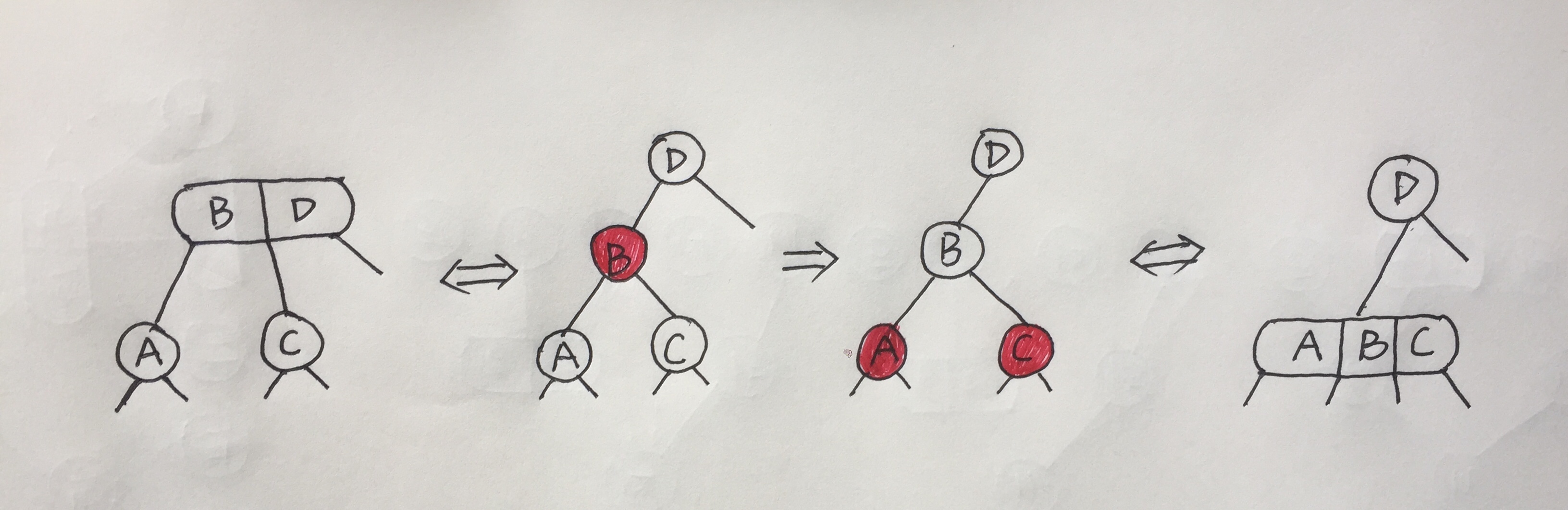

A结点的兄弟不为2-结点，可以借到结点的通用情况：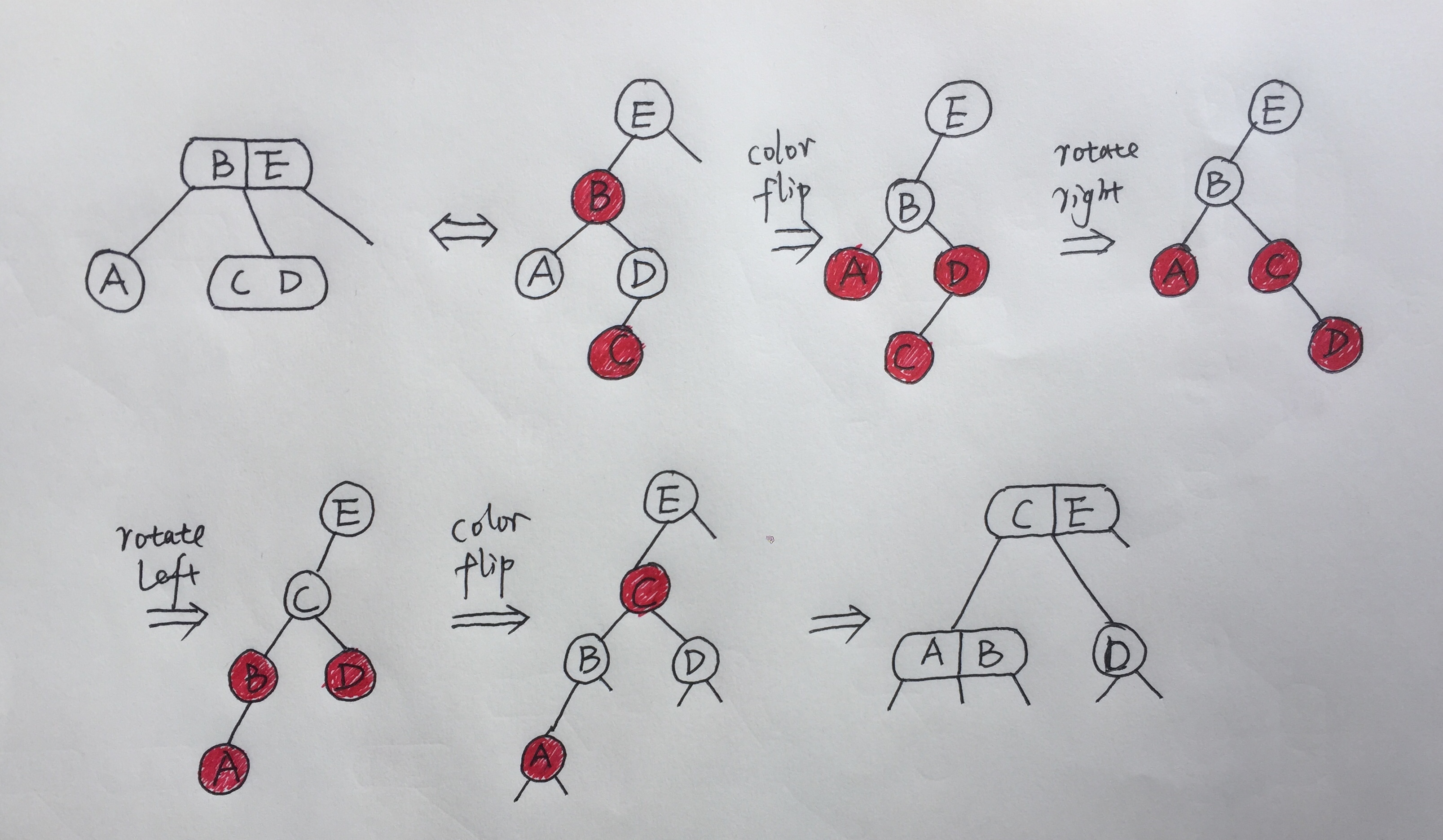

第一张图的color flip的本质是待删除结点A结点向父节点和兄弟结点借了一个结点，没有还结点给兄弟结点。
第二张图是借结点的通用过程，其中左旋和右旋的本质是用来统一保持结点的左倾红黑树，并将连续两个红结点分开掉。
如果上述两张图还没有看懂，请回到3.3节做对比。

4.3 算法导论中红黑树的算法推导

上面两张图的再细分便是算法导论中，红黑树向上修复的四种情况，其中需要说明的是，算法导论中要修复的x结点为已经删除的y结点的唯一子结点，但还要补充一点的是，在算法中x结点还代表当结点出现合并需要调整树高度时,调整子树的根结点！所以上面一直在讲的算法是先给带删除的结点补充一个结点，使结点不为2-结点时，在删除目标结点；而算法导论中的算法是先删除结点，然后在删除结点指向的结点位置修复(补充一个结点或者合并以后调整树高度)，所以大部分人被x结点指向的结点的双重黑结点所迷惑，以致于算法就更云里雾里了。这里要说明是算法导论的算法是精炼且可以严格证明的，只是讲解方法太坑人了，这也是本文的初衷。
为了避免这种混淆，我们将删除的结点标记出来，然后给带删除的结点向父节点或者兄弟结点借结点的方式描述，下图和4.2的描述没有区别，只是对应到了算法中的四种情况，如下图所示：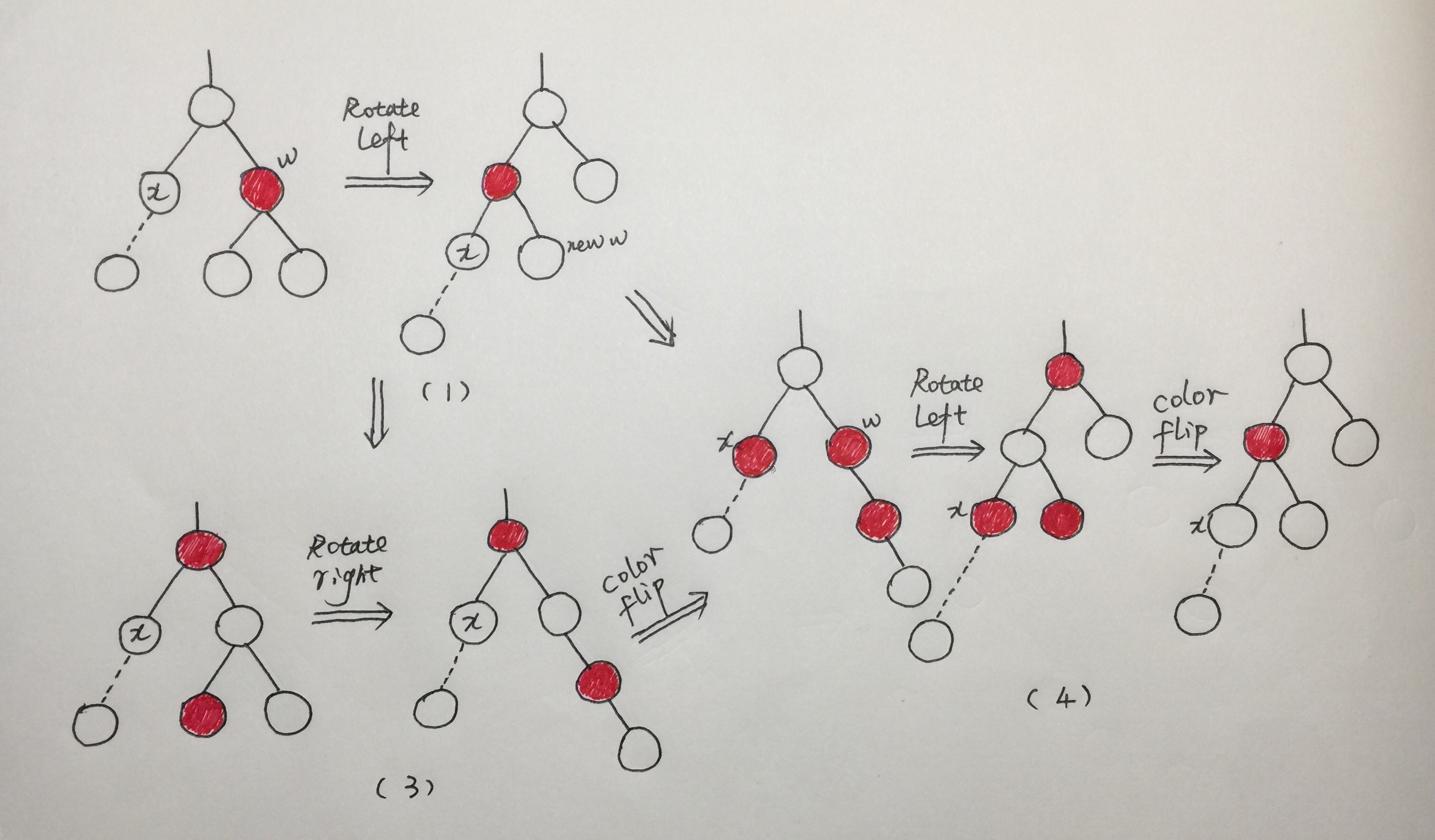

对应算法导论中的四种情况:

  • 情况1,x的兄弟w是红色的。图一,x的兄弟结点是红结点，这种情况说明父节点有结点可借，另外红结点在右边，所以选择了左旋的方式，使红结点到左边来，也使图一的情况转变成了图三和图四的情况
  • 情况3,x的兄弟w是黑色的,w的左孩子是红色。图三,x的兄弟结点的左结点是红结点，这种情况说明兄弟结点有结点可借，不过为了避免复杂，算法将他统一转为图四的情况，也就是将右倾的结点化为左倾的结点进行处理
  • 情况4,x的兄弟w是黑色的,w的右孩子是红色。图四,x的兄弟结点的有结点是红结点，同样说明兄弟结点有结点可借，这里要注意的是一次color flip就表示从父节点借到结点，旋转只是将右倾的结点转成左倾的结点。
  • 情况2,x的兄弟w是黑色的,w的两个孩子都是黑色。这种情况在2-3-4树除了借结点，还有合并结点并调整树高度的问题，算法导论中的方法是将x的兄弟结点的黑色设置为红色，然后将兄弟结点的这个黑色一直往上传递，直到可以所有子树都可以合并这个黑色。

5. 红黑树算法实现

5.1 删除逻辑

红黑树删除任意结点的算法，首先要判断结点是否是叶子结点，如果是叶子结点则可以直接删除，如果是非叶子结点，则需要找到中序遍历的后继结点作为替换结点；另外只有结点为黑色的情况才需要修正树的高度，红色的情况从2-3-4树的角度说就是不是2-结点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
bool RBTree::Delete(RBNode* z) {
	RBNode* x;
	RBNode* y;
	if (z == NULL) return false;
	if (z->left == NULL || z->right == NULL) {
		y = z;
	}
	else {
		y = this->SuccessOR(z);
	}
	// get y's only child
	if (y->left != NULL) {
		x = y->left;
	}
	else {
		x = y->right;
	}
	// remove y node
	if (x != NULL) {
		x->parent = y->parent;
	}
	// fixed y's parent
	if (y->parent == NULL) {
		m_root = x;
	} 
	else{
		if (y = y->parent->left) {
			y->parent->left = x;
		}
		else {
			y->parent->right = x;
		}
	}
	if (y != z) {
		z->key = y->key;
	}
	if (y->color == BLACK) {
		this->DeleteFixup(x);
	}
	if (y != NULL) {
		delete y;
	}
	return true;
}

5.2 中序后继结点查找
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
RBNode* RBTree::SuccessOR(RBNode* x) {
	if (x == NULL) return NULL;
    // 找到右子树的最小值结点
	if (x->right != NULL) {
		return this->GetMini(x->right);
	}
    // 也可以找到父结点的左儿子结点
	RBNode* tmp = x;
	RBNode* y = tmp->parent;
	while (y != NULL && tmp == y->right) {
		x = y;
		y = y->parent;
	}
	return y;
}
5.3 修复删除结点后树的高度

这里需要说明的是沿着x结点向上修复有x结点是父节点的左子树和右子树两种对称情况需要处理，
也就是一直未说到的删除左结点需要右边兄弟结点来补充，删除右结点需要左边兄弟结点来补充。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
bool RBTree::DeleteFixup(RBNode* x) {
	if (x == NULL) return false;
	RBNode* w = NULL;

	while (x != m_root && x->color == BLACK) {
		if (x == x->parent->left) {
			w = x->parent->right;
			if (w->color == RED) {
				// 1. case 1
				x->parent->color = RED;
				LRotate(x->parent);
				w = x->parent->right;
			}
			if (w->left->color == BLACK && w->right->color == BLACK) {
				// 2. case 2
				w->color = RED;
				x = x->parent;
			}
			else {
				if (w->right->color == BLACK) {
					// 3. case 3
					w->left->color = BLACK;
					w->color = RED;
					RRotate(w);
					w = x->parent->right;
				}

				// 4. case 4
				w->color = x->parent->color;
				x->parent->color = BLACK;
				w->right->color = BLACK;
				LRotate(x->parent);
				x = m_root;
			}
		}
		else {
			// if (x == x->parent->right)
			w = x->parent->left;
			// 1. case 1
			if (w->color == RED) {
				x->parent->color = RED;
				RRotate(x->parent);
				w = x->parent->left;
			}
			// 2. case 2
			if (w->left->color == BLACK && w->right->color == BLACK) {
				w->color = RED;
				x = x->parent;
			}
			else {
				if (w->left->color == BLACK) {
					// 3. case 
					w->right->color = BLACK;
					w->color = RED;
					LRotate(w);
					w = x->parent->left;
				}

				// 4. case 4
				w->color = x->parent->color;
				x->parent->color = BLACK;
				x->left->color = BLACK;
				RRotate(x->parent);
				x = m_root;
			}
			
		}
		x->color = BLACK;
	}
	return true;
}
点击下载完整代码

6. 参考文档