要理解数字电路,特别是同步时序电路的逻辑,首先就要了解FSM,其中两个最重要的模型就是米利模型和摩尔模型,了解这两种模型的差异,这个也是我花了很长时间去理解的地方,现在花时间记录成笔记,以备后续参考;现如今虽然已经使用verilog的硬件语言去描述,用FPGA去实现,但仍然不能离开其数字电路理论的根本,这个是要扎实去掌握.
1. Mealy(米利)和Moore(摩尔)模型主要区别
- 摩尔模型的状态数量一定大于米利模型,但摩尔模型的一个状态对应一个输出
- 米利模型状态少,但一个状态可以对应多个输出
2. 例子说明
自动售货机投入1元5角时送出一杯饮料;投币前的状态最多是已经投了0,5角,1元,当前状态可以投入0,5角,1元;
米利模型
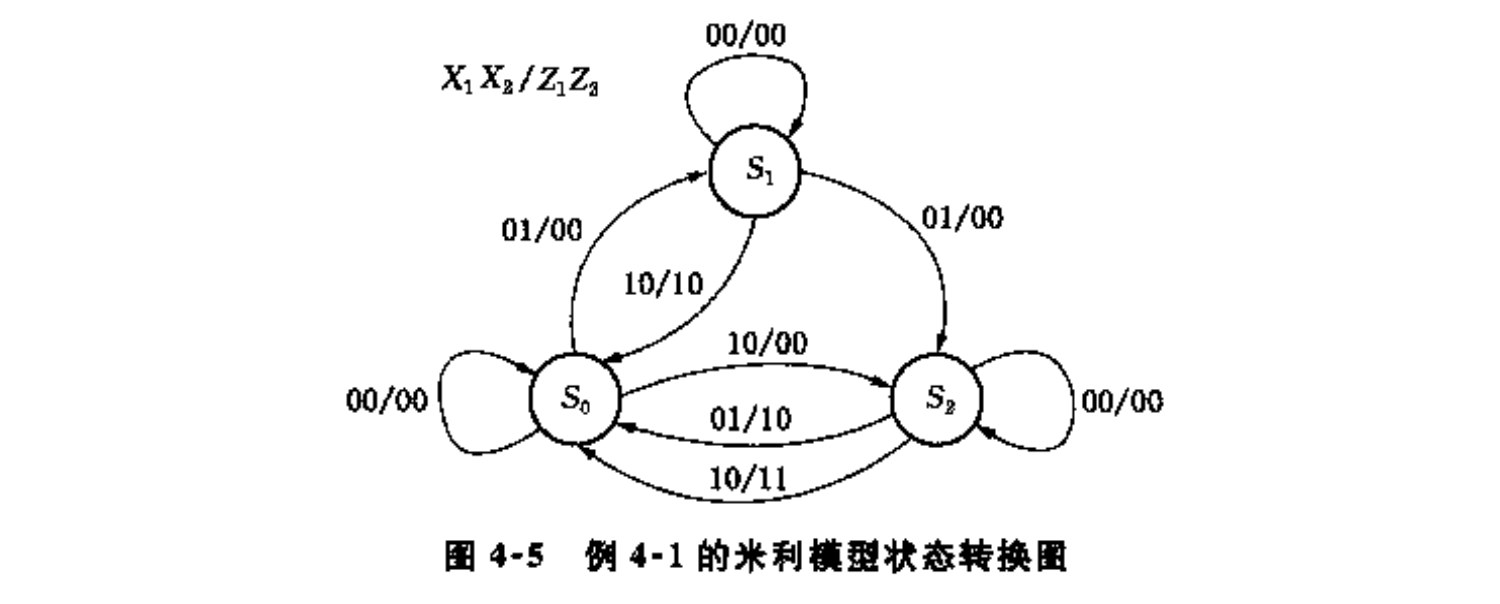
- $X_1X_2$,使用00,01,10,分别表示0,5角,1元的投币(表示当前输入);
- $Z_1=1$表示出饮料,$Z_2=1$表示找零(输出);
摩尔模型
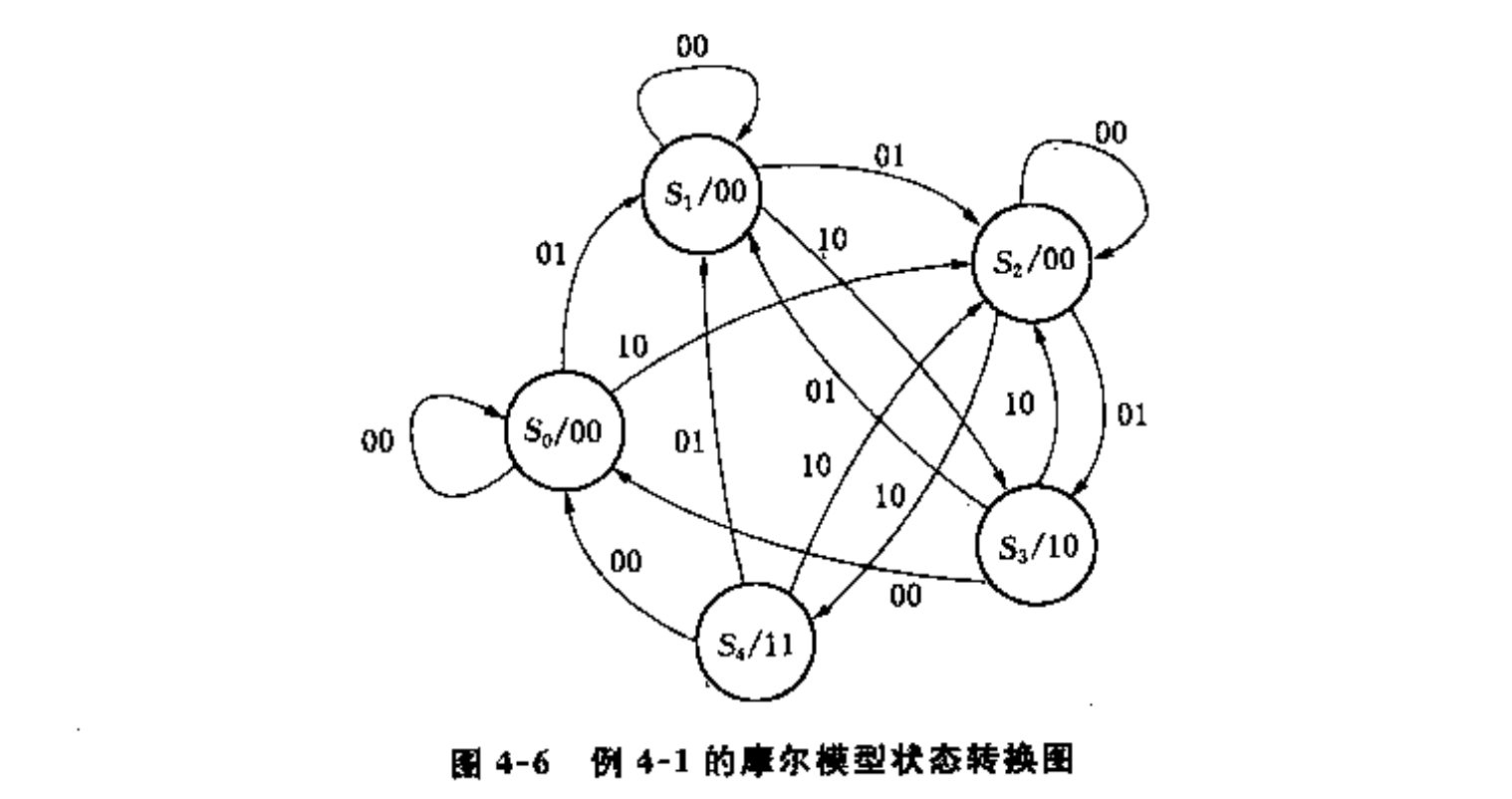
- S0~S4分别表示0,5角,1元,1元5角,2元(当前态)
- $Z_1Z_2$,$Z_1=1$表示出饮料, $Z_2=1$表示找零;(输出,图中S0/$Z_1Z_2 $)
- $X_1X_2$,使用00,01,10,分别表示投币0,5角,1元的投币(输入,箭头上方的数字)
3.相互转换(重点)
摩尔模型转米利模型
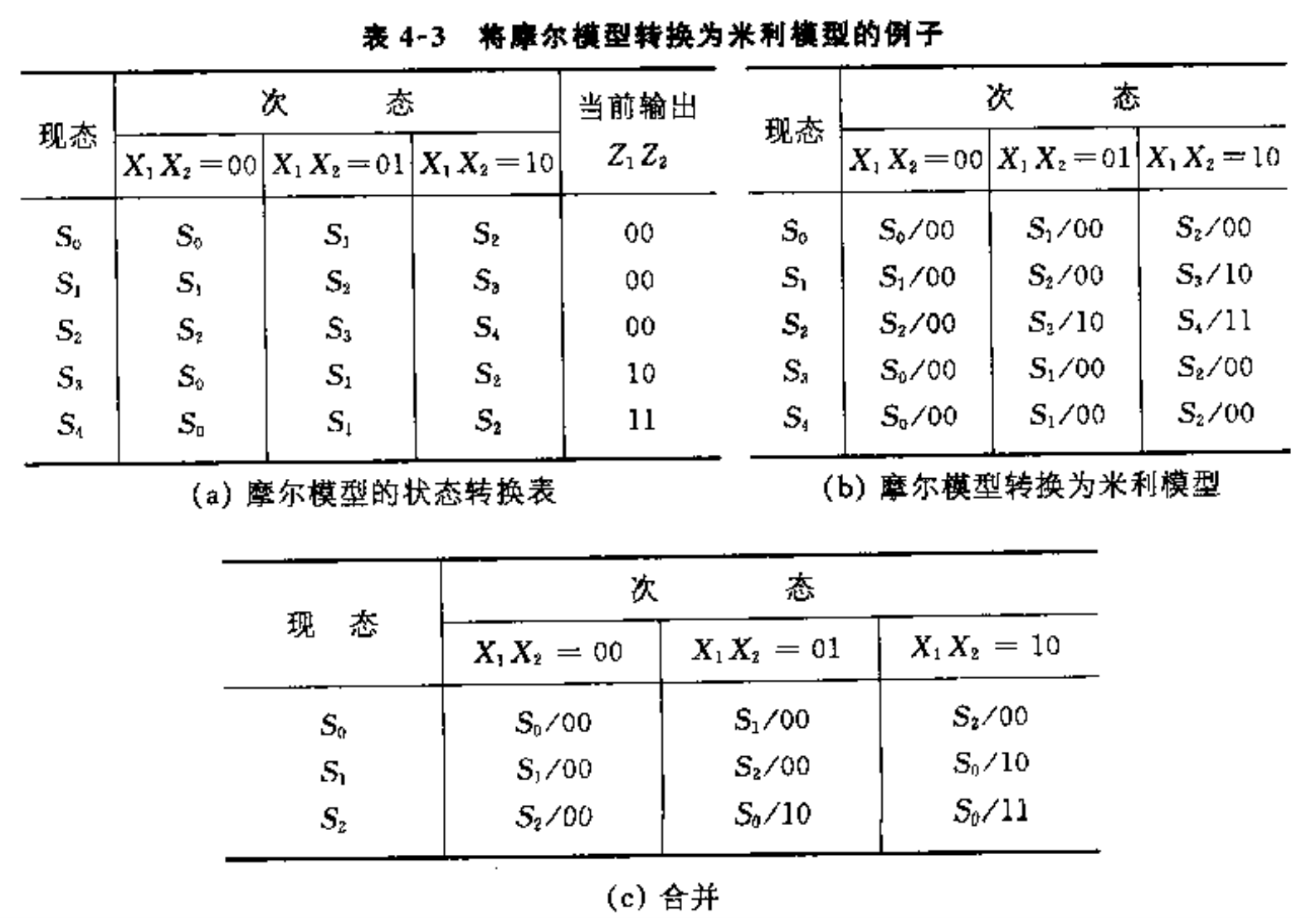
要点: 在每个次态的后面增加现态所对应的输出;比如$S_4$的当前输出是$Z_1Z_2=11$;那么现态为$S_2$的$X_1X_2$列输出更改为$S_4/11$;去掉转换表的输出列;
米利模型转摩尔模型
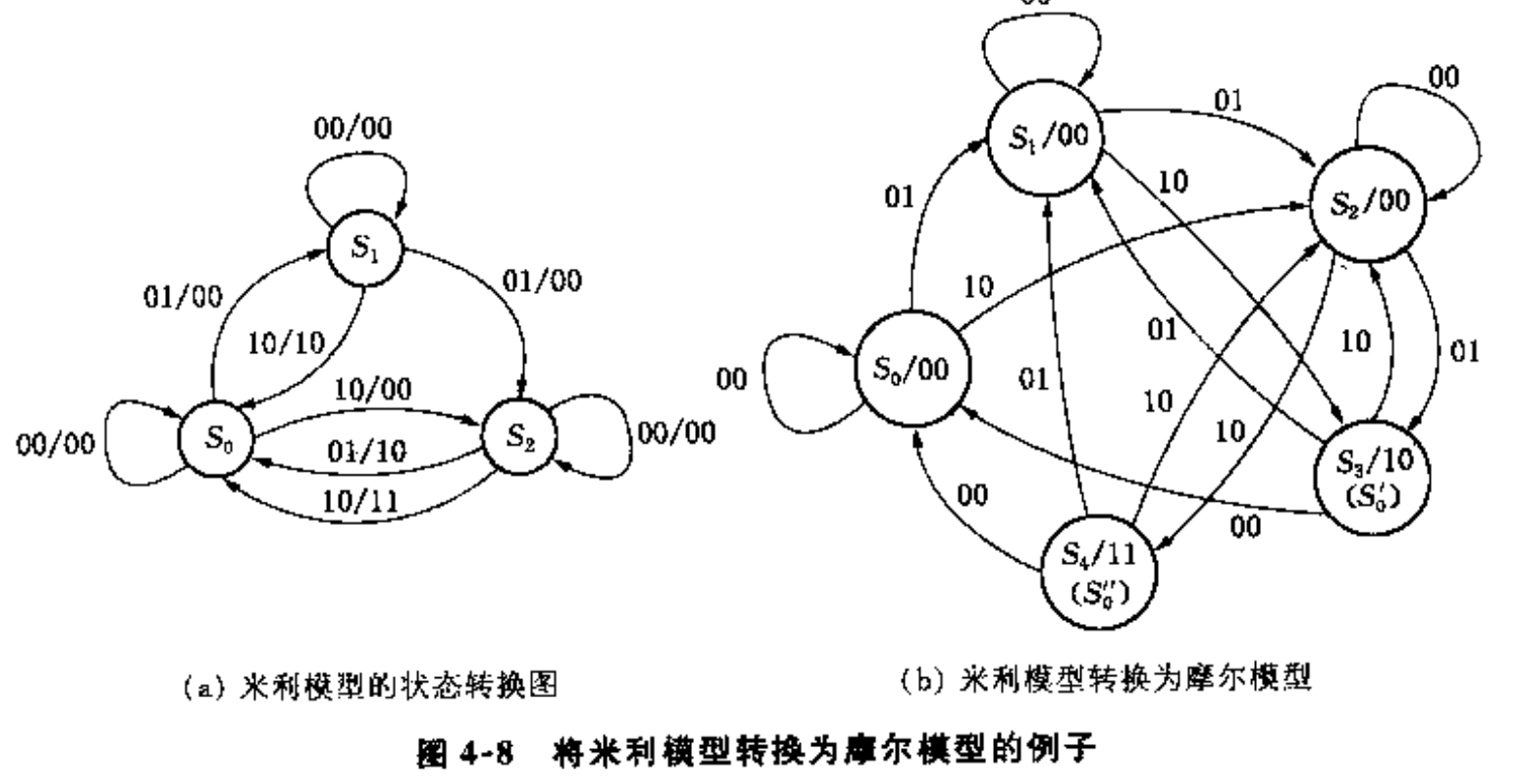
要点: 在米利模型中要找出一个状态下,不同的输入对应多个不同输出的情况;比如$S_2$到$S_0$的状态转换,涉及到两种输入一种是01/10,一种是10/11的输入,不同的输入/输出却对应相同的状态,应该将这种状态分离出来,这两个就是新增的状态;
总结:现在在大多时候进行同步时序电路设计时已经不用进行模型设计,但是能不能用算法状态机设计同步时序电路也是需要一定的基本功,可以试试比如手写推导一个4位的全加器.