电子03-并联谐振详细推导

并联谐振电路是高频小信号电路的选频电路,不完全理解并联谐振电路的特点,后续的内容你就无法理解;本文先推导并联谐振频率的过程;然后品质因数和通频带进行推导,其中通过谐振曲线公式的推导,更能理解这个电路参数在选频电路中的特征;为后续的分析打下坚实的01基础,写作本文是为了后续容易回顾推导过程和其中的不足.

1. 谐振频率推导

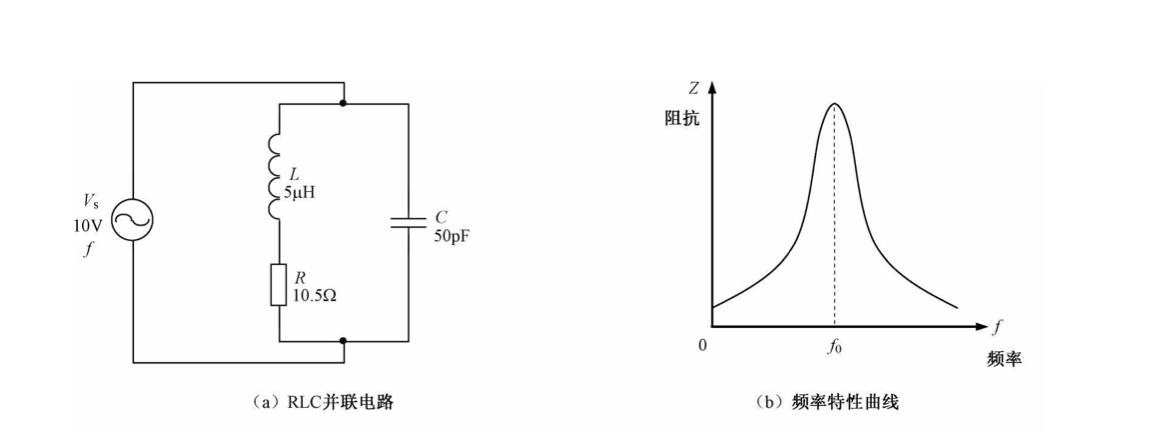
参考前一章$X_cX_L的表示$复数表示形式: $X_L = j\omega L \quad\quad X_c = - j\frac{1}{\omega C}$

根据上面电路得出阻抗公式:

$Z = \frac{(R + X_L)* X_C}{(R +X_L) + X_C} = \frac{(R +j\omega L) * - j\frac{1}{\omega C}} {R + j\omega L-j\frac{1}{\omega C}}$

第一种情况
$\omega L >> R $ 时忽略R的阻值,注意上面公式 $j\omega L * - j\frac{1}{\omega C} = \frac{L}{C}$ 其中 $j^2=-1$

上面的推导重点说明两个内容
- 一个是并联谐振时虚部值为0,整个电路成纯电阻型: $\omega C-\frac{1}{\omega L} = 0 \Rightarrow \omega C = \frac{1}{\omega L} \Rightarrow {\omega}^2 = \frac{1}{LC} \Rightarrow \omega_0 = \frac{1}{\sqrt{LC}}$
- 另外一个是阻抗的倒数是导纳 $Y = G +jB = \frac{1}{Z}$ 这个是解释一个问题就是当电路谐振时电路的导纳为$Y= G_0 = \frac{CR}{L}$,后面要一直用到,对应上面的Z公式部分就是 $G = \frac{CR}{L}\quad\quad B =\omega C - \frac{1}{\omega L}$
第二种情况
就是不能忽略R的电阻值的计算推导

以上就是关于并联时的谐振频率的推导,谐振频率跟LC直接相关.

2. 品质因数

品质因数的定义就是这个电路的阻抗和纯电阻的比值;这个值说明这个电路选择频率的好坏就是值越大选择性越好,当然也就是带宽越窄。

$Q_0 = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 CR} = \sqrt{ \frac{\omega_0 L}{R * \omega_0 CR} } = \frac{1}{R} * \sqrt{ \frac{L}{C} }$

得出的结论竟然是品质因数竟然是个常数,只跟RLC的值有关.可以想到的是这个是在谐振频率的时候,不在谐振频率的时候整个电路的阻抗为感抗或者容抗的 $Q_0$倍

3. 谐振曲线

回路电压幅值与外加电压频率之间关系曲线称为谐振曲线.Z的公式带入到下面的公式里:

$\dot{V} = \dot{I_s}Z = \frac{ \dot{I_s} \frac{L}{C}}{ R = j(\omega L - \frac{1}{\omega C})} = \frac{ \dot{I_s} \frac{L}{CR}}{ 1 + j \frac{ \omega L - \frac{1}{ \omega C}}{R}}(同时除以R)$

在谐振频率推导时说$Z_0$;在品质因数一节中推导时说的$Q_0$;将下列公式带入上面的公式:

$G_0 = \frac{CR}{L} \Rightarrow Z_0 = \frac{L}{CR} \quad\quad Q_0 = \frac{\omega_0 L}{R} = \frac{1}{\omega_0 CR}$

带入公式中:

$\Rightarrow \dot{V} = \frac{\dot{I_s}Z_0}{ 1 + jQ_0(\frac{\omega L}{R} * \frac{R}{\omega_0 L} - \frac{1}{\omega CR} * \frac{\omega_0 CR}{1})} = \frac{\dot{I_s}Z_0}{1 + jQ_0(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega})}$

上面公式下半部分的推导:

$\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega} = \frac{\omega^2 - \omega_0^2}{\omega_0\omega} = (\frac{\omega + \omega_0}{\omega})(\frac{\omega - \omega_0}{\omega})$

当 $\omega$ 与 $\omega_0$ 很接近时:

$\Rightarrow \approx \frac{2\omega}{\omega}(\frac{\omega - \omega_0}{\omega_0}) = 2(\frac{\omega - \omega_0}{\omega_0}) = 2\frac{\Delta{\omega}}{\omega_0}$

得出实时电压和调谐时电压比(复数形式)
其中 $\dot{I_s}Z_0 = \dot{V_0}$ $\frac{\dot{V}}{V_0} = \frac{1}{1 + jQ_0(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega})}$
得到比值参考复数转换成角度形式 $\frac{V}{V_0} = \frac{1}{\sqrt{ 1+ [Q_0(\frac{\omega}{\omega_0} - \frac{\omega_0}{\omega})]^2}} \approx \frac{1}{ \sqrt{1 + (Q_0 \frac{2\Delta\omega}{\omega_0})^2}}$

4. 通频带

以下是我自己的理解:上面的公式得出的结论是并联谐振电路时,谐振的品质因数和谐振频率是固定的,但是信号源的频率往往和谐振频率有一定的偏离,导致电压发生一定的变化,这里变化的范围就是上面公式中分母部分的 $\xi = Q_0 \frac{2\Delta\omega}{\omega_0} $;推导出来的频率的变化范围只能是 $Q_0 \frac{2\Delta\omega}{\omega_0} = 1 \Rightarrow 2\Delta\omega = \frac{\omega_0}{Q_0}$

这个$2\Delta\omega$就是通频带,看上去也是一个常数.

后记：自学高频电路纯属在学完模拟电路以后的一个扩展,相当难啃;但是所有的知识点就像一块块拼图,要知道后续的原理必须慢慢来,一块一块拼好,上面的内容没有考虑实际电路中的比如信号源内阻和负载内阻的情况;不过基本的分析思路是根据上面的过程来进行