咖啡's blog

专心 专注 专业

0%

AES加密算法3-乘法逆元实现

发表于 更新于 分类于 ， Valine：

这里实现的是GF(2^8)域的扩展欧几里得算法求乘法逆元。这里涉及除讲过的有限域乘法,这里还有有限域除法,先记录一下有限域除法实现,然后根据扩展欧几里得算法,求出对应数的乘法逆元.

1. 有限域$GF(2^8)$除法

根据除数与被除数最高位的差距d,使除数左移d与被除数减(XOR).如下图所示:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 找到当前val的最高位的索引
uint8_t search_high_bit(uint16_t val) {
    uint8_t i = 0;
    while (val) {
        ++i;
        val >>= 1;
    }
    return i;
}

uint8_t gdiv(uint16_t a,uint16_t b,uint16_t* remainder) {
    uint16_t r0 = 0;
    uint8_t qn = 0;
    int cnt = 0;
    r0 = a;

    uint8_t x1 = search_high_bit(r0);
    uint8_t x2 = search_high_bit(b);
    // cnt是有可能小于0的
    cnt = x1 - x2;

    while (cnt >= 0) {
        // 商的表示形式
        qn |= (1 << cnt);
        // 加或者减就是XOR
        r0 ^= (b << cnt);
        // 重新计算可用的商
        x1 = search_high_bit(r0);
        cnt = x1 - x2;
    }
    //余数
    *remainder = r0;
    return qn;
}

2. 扩展欧几里得算法实现

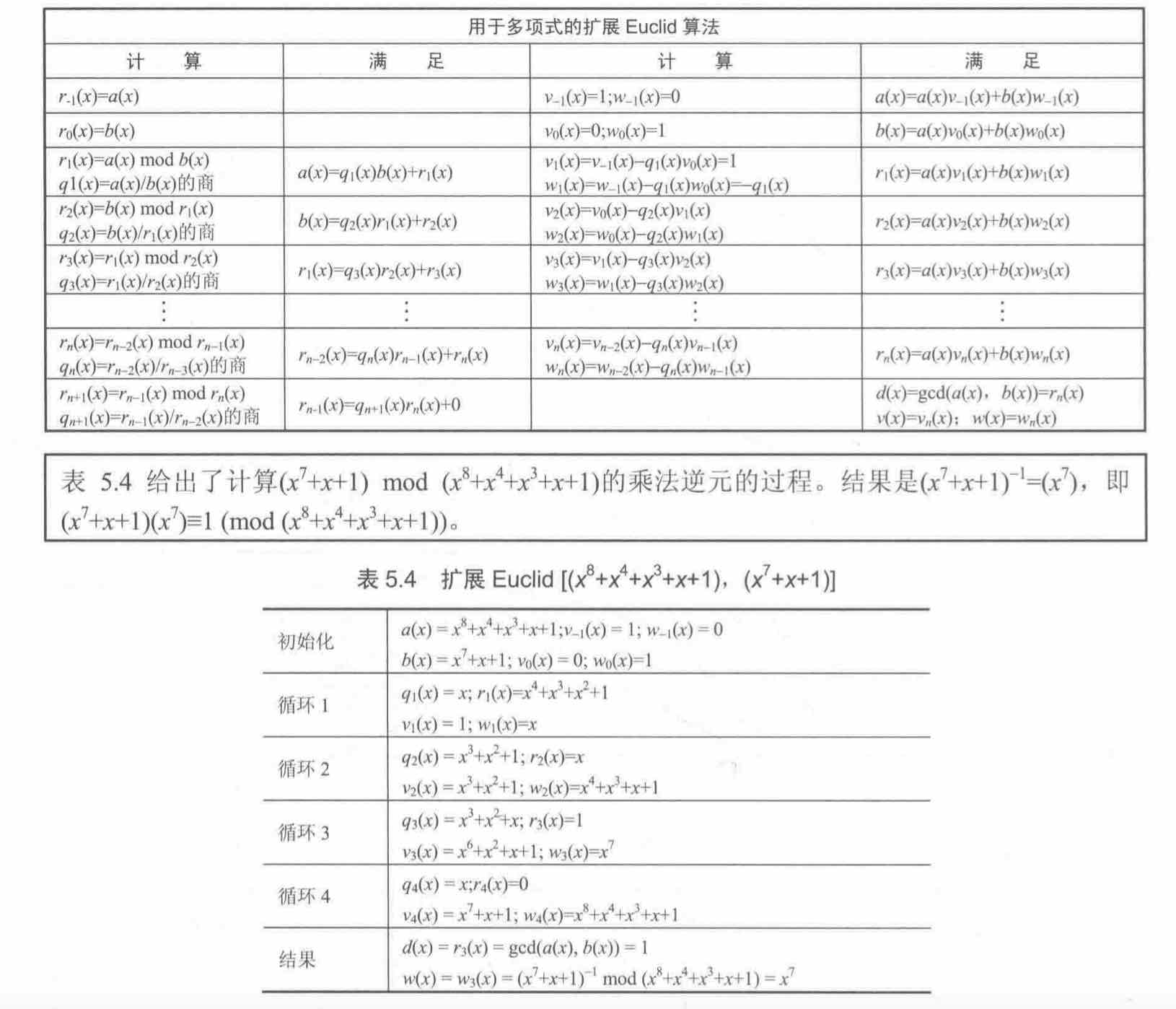
根据上面这张表格设计算法,这一张表格只不过是乘法逆元推导的扩展到多项式应用,其中用到了有限域$GF(2^8)$的除法和余数。代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
uint8_t gmult_inverse(uint16_t a,uint16_t b) {
    uint16_t r0 = 0,r1 = 0,r2 = 0;
    uint8_t qn = 0,v0 = 1,w0 = 0,v1 = 0,w1 = 1;
    uint8_t v2 = 0,w2 = 0;
    // 上图中b初始值为0x11b; // x^8 + x^4 + x^3 + x + 1
    // a初始值为0x83; // x^7 + x + 1
    r0 = b;
    r1 = a;
    // gcd(a,b) = 1
    while (r1 != 1) {
        // 计算r1 | r0的商qn和余数r2
        qn = gdiv(r0, r1, &r2);
        // 对应上图的第三列
        v2 = v0 ^ (gmult(qn,v1));
        w2 = w0 ^ (gmult(qn,w1));
        // 迭代
        r0 = r1;
        r1 = r2;

        v0 = v1;
        v1 = v2;

        w0 = w1;
        w1 = w2;
    }

    return w1;
}

3. 验证一下

使用上图的例子计算乘法逆元.

1
2
3
4
5
6
7
8
9
10
11
int main() {
    /// 0000 0000 1000 0011
    uint8_t a = 0x83; // x^7 + x + 1
    // 0000 0001 0001 1011
    uint16_t b = 0x11b; // x^8 + x^4 + x^3 + x + 1
    // 计算乘法逆元
    uint8_t R = gmult_inverse(a,b);
    // 1000 0000
    printf("gmult_inverse :%x\n",R); // x^7 = 0x80
    return 0;
}

总结: 被除法的最高位与除数的最高位差,实际计算过程中是存在小于0的情况,可以参考下述手动演算截图的最后一步,而倒数第二步是等于0的情况;在扩展欧几里得计算的第一步中,$r_0$的初始值为$ x^8 + x^4 + x^3 + x + 1$,这个值实际是超过了GF(2^8)的域的。

附录：