AES加密算法2-乘法逆元推导

AES加密里有一个S盒,构造这个S盒中需要使用到有限域$GF(2^8)$的乘法逆元的计算,推导乘法逆元的计算首先是从求最大公约数开始的,然后讨论了模运算的性质,利用模运算的性质证明可以使用欧几里得算法求最大公约数,然后将欧几里得算法推广到有限域上;

1. 乘法逆元概念

如果一个代数式$F$乘一个数a后，再乘它的倒数 $\frac{1}{a}$，相当于没有乘a （这里不考虑0的情况），换句话说，我们乘$\frac{1}{a}$后，取消了代数式 $F$ 乘a后值增大的影响。

正式的定义是这样的:如果说 $a$ 在模p意义下的乘法逆元是 $x$,那么 $ax \equiv 1(mod)p$ ,推广到有限域上以模8运算为例,如下图: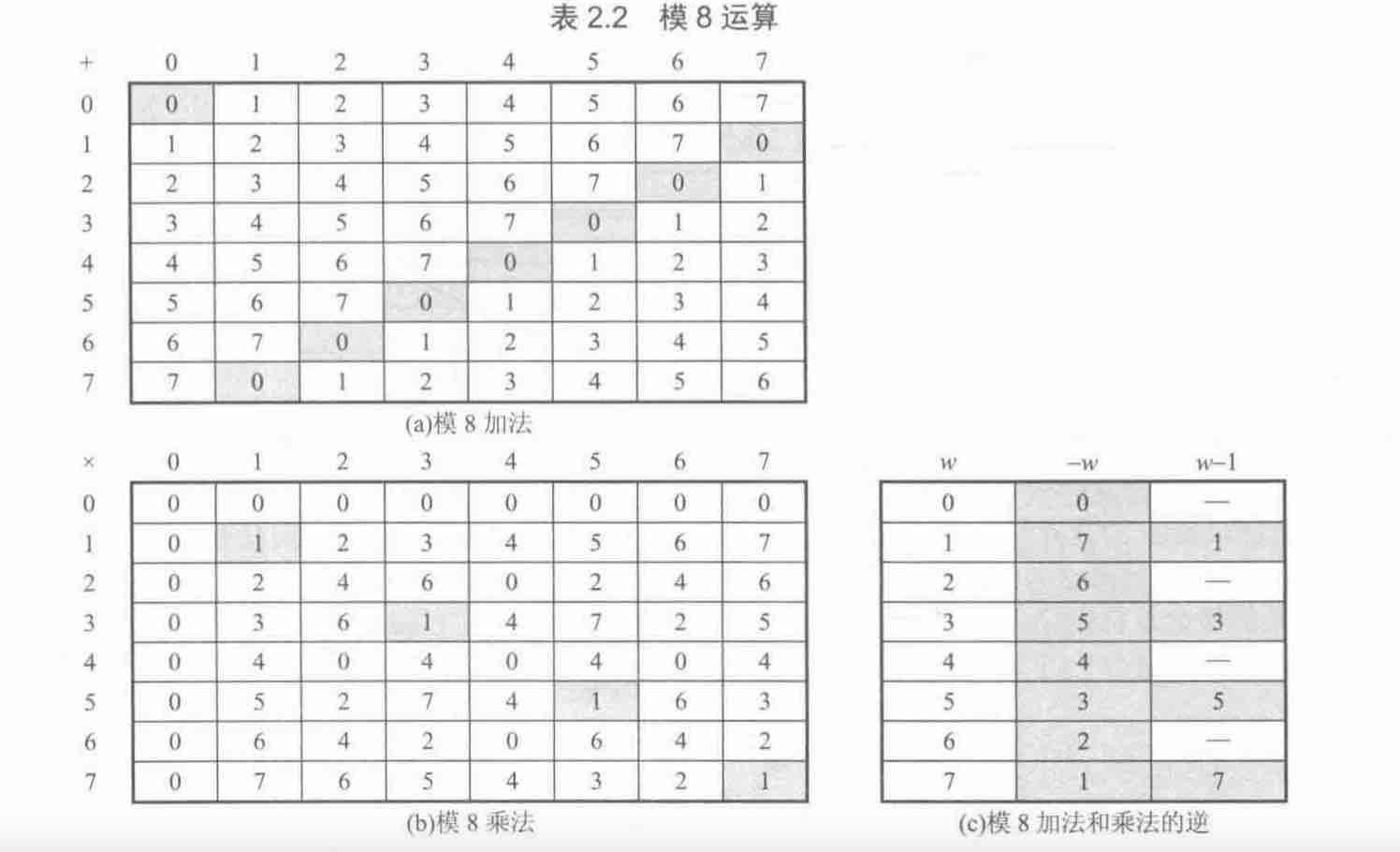

模8乘法表中值为1的横轴和纵轴: (1x1)mod 8 = 1;(3x3)mod 8=1;(5x5)mod 8=1;这里就是要说明1和1,3和3,5和5在模8下是互为乘法逆元。

2. 乘法逆元推导

最大公因数: a和b的最大公因数为能同时整除a和整除b的最大整数,记为$d = gcd(a,b)$.
整除性的一个推导:
结论:对任意整数m,n，若$d|a$且$d|b$,则可得 $d | (ma+nb)$

证明:
$ d|a \Rightarrow a = d\ast{a_1} \quad\quad d|b \Rightarrow b = d\ast{b_1}$

$ ma + nb = md\ast{a_1} + nd\ast{b_1} \Rightarrow d | (ma + nb)$
求最大公因数推导
b除a可以表示为 $ a = q_1b + r_1$
- 当$r_1=0$时,$d = gcd(a,b) = b$(表示a能被b整除);
- 当$r_1\ne0$时,将上面整除性的推导的m=1,$n=-q_1$代替,推导出$d | (a-q_1b) \Rightarrow d | r_1 $(备注:$r_1 = a - q_1b$),得出的结论是 gcd(a,b) = gcd(b,r1) = d ;这里就是用带余除法求出最大公因数,也就是余数最后至少可以被1整除.计算实例如下:
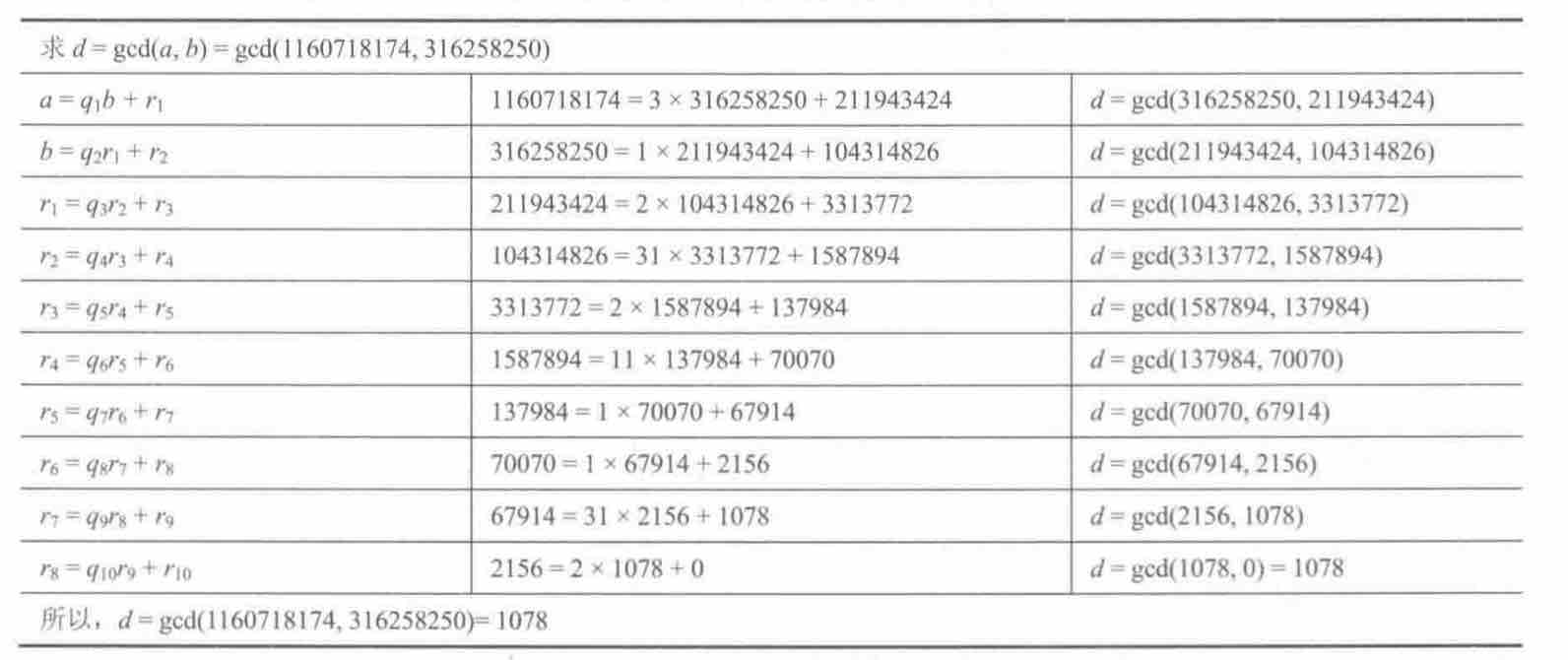
推导出欧几里得算法
将上面的余数$r_1$用模运算表示就是 $ r_1 = a\mod b$,所以求最大公因数的递归算法如下,对比上图看,上图的第一列对应下图的第二列,下图的第一列对应于上图的最后一列里gcd算式的第二项,因为$gcd(a,b) = gcd(b,a\mod b)$
扩展欧几里得算法
扩展欧几里得算法主要是为了给定两个整数a,b,除了找到这两个数的最大公因数外,还要找到两个数x,y,满足$ ax + by = d = gcd(a,b)$,计算推导过程如下: 推导过程虽然比较冗长但是非常重要,所以放在这里,这里主要注意的是求$x_i$和$y_i$,只跟$q_i$,i-1和i-2步的计算结果相关.列出表如下：
3. 求乘法逆元
乘法逆元的定义 $ax \equiv 1(mod) p$ $\Rightarrow ax\mod p = 1\mod p$ $\Rightarrow (ax - 1)\mod p = 0$ 设p的k倍,使下列等式成立: $ax - 1 = k\ast p$ $\Rightarrow ax - k\ast p = 1$